LAST POST

THIS IN THEORY IS THE LAST POST IN THIS BLOG!

Activity 19: Restoration of Blurred Images

Objectives: To demonstrate the concept of motion blur and its restoration as well as basic noise filtering.

Tools: Scilab with SIP toolbox.

Procedure: We begin with an ordinary image with text written on it, in this case we use a grayscale image of the Apollo 13 Mission Patch with the words "Apollo XIII" and "Ex Luna Scientia."

We are in theory to simulate motion blur using the equation:

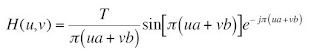
However, some difficulty was encountered in implementing this. As such the images were blurred using Photoshop, with varying distances of blur. After this, we add noise to the blurred image using the Gaussian image routine established in the previous activity, resulting in image like the one below:

Then using the filtering method described in the activity, Weiner filtering, the original image is reconstructed using different parameters. The working equation is given as:

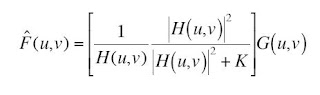
The reconstructed images for the middle sample above (with medium blur) follow:

Interestingly, the filtering routine seems to have worked even if the blurring functions used are of uncertain similarity. It appears that the blurring routine used in PS is similar to the routine we are to use here, but of course the correlation may be purely coincidental.

Evaluation: For the properly reconstructed images a grade of 10 is proper.

Acknowledgements: As usual Mr. Cabello and Panganiban have rendered invaluable assistance in this activity.

Activity 18: Noise Models and Basic Image Restoration

Objectives: To demonstrate basic noise modelling and the removal of noise from images using filters

Tools: Scilab with SIP toolbox, grayscale test and sample images

Procedure: We begin with a grayscale image of three gray levels from white to black. Simultaneously we use a real world image (in this case a grayscale image of the Apollo 13 Mission Patch) with more than three gray levels.

We model the different types of noise using mathematical models presented and add these noise matrices to both the test image and the real-world image. The following plate shows the images with different noise models added:

From top to bottom, the noise models are: Exponential, Gamma, Gaussian, Salt and Pepper, Uniform and Rayleigh noise. The added noise is then filtered on all the images using a variety of filters, described in the text (Arithmetic mean, Geometric mean, Harmonic mean and contraharmonic mean filters). The images above are processed using each of these filters and the results are shown below for each of the added noise types:

1. Exponential Noise

2. Gamma Noise

3. Gaussian Noise

4. Salt and Pepper Noise

5. Uniform Noise

6. Rayleigh Noise

Evaluation: For correct noise models and filtering a grade of 10 is acceptable.

Acknowledgements: I would like to thank Mr. Panganiban for the invaluable assistance in this activity.

Activity 17: Photometric Stereo

Objectives: To reconstruct a three dimensional image using a set of 2-D images with different illumination positions.

Tools: Scilab with SIP.

Procedure: We start with four images of a spherical calibration target illuminated by a point source at these locations:

S1 = (0.085832, 0.17365, 0.98106)

S2 = (0.085832, -0.17365, 0.98106)

S3 = (0.17365, 0, 0.98481)

S4 = (0.16318, -0.34202, 0.92542)

The positions vary by very small increments and hence the images do not appear to be any different to the eye. We find the surface normal vector to the points on the surface using the equation:

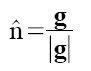
Where g is given by:

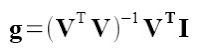
With V taken from the images. The slope with respect to z of each point in both x and y is given by:

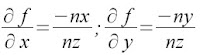
The function f is fiven by the sum of the integrals of the partials in x and y. Numerically we use the cumulative sum fucntion to find these integrals and the resulting funtion is plotted in 3-D. The result is somehting like the plot below:

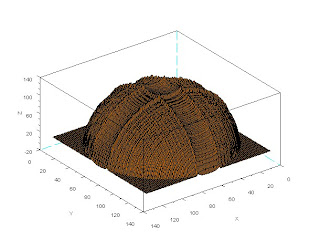
As we can see, the plot is hemispherical which is the result expected. It is of interest to examine the effect of varying the illumination shift on the accuracy of the reconstruction. It is also of note that this approach is from the stanpoint of intensity. That is, the changes in the illumination allow for the measurement of slope and shape. Another approach may involve the phase of the illuminating light which has been shown to yield better results in terms of reconstruction ability.

Evaluation: For the proper reconstruction of the shape, a grade of 10 is appropriate.

Acknowledgements: The assistance of Neil Cabello and Earl Panganiban is greatly appreciated.

Activity 16: Neural Networks

Objectives: To demonstrate the application of neural networks in pattern recognition

Tools: Scilab with SIP and ANN toolboxes

Procedure: As most of the details of the procedure are canned and those which are distinct are graphically repetitive, we shall go through what was done only in broad sweeping strokes. As mentioned, we used canned code for this, available through various channels. We first set a seed for consistency. We then create a training set of several values of two parameters, in this case as before, the area and red-color channel value of the intensities. For example we utilize the set:

y=

0.04 0.44

0.05 0.41

0.07 0.45

0.18 0.43

0.21 0.45

0.33 0.44

0.36 0.42

0.38 0.43

For this set, we classify this, in a manner similar to Boolean, as

[ 0 0 0 0 0 1 1 1]

That is to say, for our purposes, the last three sets, with the corresponding parameters are the ones to be classified under a certain heading and all the others effectively discarded.

Now we define a test set of object parameters we wish to classify:

x=

0.20 0.44

0.23 0.45

0.40 0.41

0.38 0.39

0.36 0.40

0.04 0.41

0.05 0.42

0.24 0.40

0.37 0.41

0.39 0.39

0.38 0.42

0.36 0.38

0.39 0.45

0.06 0.35

0.22 0.33

0.38 0.40

0.40 0.39

0.37 0.38

0.02 0.31

0.04 0.34

The output of the code, at a learning rate of 1 and with 1000 training cycles,rounded off to the nearest integer (1 or 0) is

[ 0 0 1 1 1 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0]

Which is in exact agreement with what is expected. It is of note that when the learning rate is decreased, the pointwise accuracy of the network decreases. Additionally, the training cycle also has the same direct effect which agrees with intuitive understanding.

Evaluation: For proper classification a grade of 10 is appropriate.

Acknowledgement: As usual, Mr. earl Panganiban is of mention for his assistance.

Activity 15: Probabilistic Classification

Objectives: To apply Linear Discriminant Analysis to classify and sort objects from two distinct classes.

Tools: Scilab and data from Activity 14.

Procedure: The aim of the activity is to classify the objects in an

image into distinct groups in much the same way as the previous activity. Instead of using the distance method, we use linear discriminant analysis or LDA, the details of which can be found elsewhere. We utilize the same set of images from the previous activity, that of the coins.

As mentioned the data from the previous activity is used with same classification characteristics, that is area and color. Since we want to examine the usage of LDA on two classes of objects only, we sort our data set according to area and exclude the first ten values, as these correspond to one class of objects. This is to eliminate the need to mask one of the object test classes and redoing the image processing routines.

We then apply the LDA routine per the tutorial provided and plot in two axes, we get a figure similar to the previous activity. The crosses represent the loci of the objects in the image with respect to area and color.

Note the distinctive separation of the two classes with the lower set representing the lower denomination coins. Also of note is the better discrimination between the two classes compared to the previous activity. In the said procedure, the distinctions between two almost similar classes is unclear. In this case the deliniation is much clearer and hence it can be expected that this method will yield a better grouping and classification result.

Evaluation: For the proper classification of the objects a grade of 10 is appropriate.

Acknowledgements: The usual thanks to Neil Cabello and Earl Panganiban for the unfailing assistance.

Activity 14: Pattern Recognition

Objectives: To demonstrate the application of pattern recognition in describing a set or ensemble of objects in an image.

Tools: Scilab with SIP, an assembly of items with differnt shapes and sizes

Procedure: We begin by assembling a set of 30 coins representing our test objects. We use 10 each of .25, 1 and 5 Peso coins. The size of these coins increase with their denomination hence we can use that as one of our test parameters. Also the coins have different colors with the 25-centavo coin being bright copper, the one having a silver color and the 5 having a dull yellow-green tinge. We first take five of each coin and take a picture which we will use as our training set.

We then use a binarized copy of the image to find the areas of the coins using bwlabel. We do this for all the coins in the training set and group the similar values together. We then take the first five values and find the average which will then represent the average area of the one-peso coin. We do this for the next two sets of fives to get the areas for the other two coins. Then using the original image, we find the red-channel colors of each of the coins and in a similar manner find the average values. These two values, the area and the color represent our classifiation parameters which we then apply to a test set consisting of 10 coins of each denomination. arranged randomly within the field.

Using the same processing scheme as with the training set sans the averaging segment, we find our two classification parameters from the image and plot this with the x-axis being the area and the y-axis representing the color values of the red-channel.

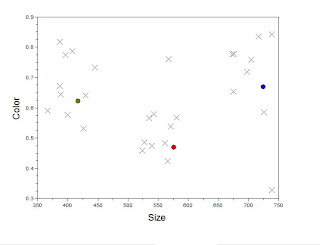
Note that the cirlces represent the training parameters, that is the average color and area of each of the coins. We see a good clustering of the test points around the training values in the x-axis. This means that in terms of area, the coins in the test sample are quite distinguishable. However we still see a deviation from the ideal area which we can attribute to the changes in the area caused by the conversion from RGB to binary of the area measurement. Some of the coins shrink or expand depending on the lighting conditions and the thresholding value. Similarly in the y-axis we see a greater deviation from the average color values which again may be attributed to the lighting. Notice that the test and training images do not have exactly identical lighting conditions. As such some degree of deviation is expected. Of course this can be alleviated by employing more consistent lighting or in some cases, adding more features to test.

Evaluation: For the generally accpetable results, a grade of 10 is warranted.

Acknowledgements: The invaluable assitance of Mr. Earl Panganiban is greatly appreciated and is key to the completion of this excercise.

Activity 13: Correcting Geometric Distortion

Objectives: To demonstrate the process of correcting geometric distortions present in images.

Tools: Scilab with SIP.

Procedure: In order to simplify the computation, we use a grid of horizontal and vertical lines with barrel distortion present like the one we have below:

Using an idealized matrix of points, that is in the proper perpendicular vertex loci which is derived either using software or manually through the interface, we establish our reference grid. This is represented as a set of points occurring on the intersections of the lines.

Now using the least distorted part of the test grid image, we compute c1 through c8 using the following matrices:

Using linear algebra, the details of which we will omit as they are redundant, we get an expression for the coordinates of all the points of the image translated into the undistorted or proper frame:

This gives us the coordinates of the vertices in the correct frame. We use 2 interpolation methods to generate the points in between. We first use the bilinear interpolation which yields a grid like:

And then using the nearest neighbor interpolation we get:

As is consistent with theory, the bilinear method yields better results in terms of reconstructions.

Evaluation: For the properly reconstructed grid, a grade of 10 is justified.

Acknowledgements: As usual I thank Earl Panganiban and Gilbert Gubatan for their assistance.

Activity 11: Color Camera Processing

Objectives: To demonstrate the principle of color balancing in color cameras especially the post recording correction of improperly color balanced images.

Tools: Scilab with SIP toolbox

Procedure: We begin with several improperly color balanced images with several objects of different colors present. These have their color balance settings varied to show the effects of white balancing.

The right panel shows the result of the correction using the white patch algorithm. The images below show a drastically wrongly color balanced image corrected using both the white patch and grayworld algorithms

As can be seen from the images, the correction for both algorithms is generally acceptable. The white patch has more color fidelity especially in the red region while the grayworld is more uniform. However, for images which are dominated by a ceratin color, the gray world algorithm fails in that it generally overcorrects for a complimentary color. Hence, the white patch algorithm is a better all around method.

Evaluation: For the partially completed work, a grade of 7 is the highest appropriate score, as the algortihms were already implemented.

Activity 10: Preprocessing Text

Objectives: To apply image processing methods to isolate handwritten text from an imaged document.

Tools: Scilab with SIP toolbox

Procedure: We begin with a scanned image of text both handwritten and in type. Since the image is tilted, we make it upright using the mogrify() command in Scilab. For computing expediency we also resize the image to more managable dimensions.

We then crop a small portion of the image, with handwritten text to isolate then convert this to grayscale. Taking the FT as shown in the center image below allows us to see the components that we do not need, in this case the bright vertical line at the center corresponding to the horizontal lines on the image. Using a mask like the one on the right we can cancel this component out.

After eliminating the lines, we clean the images using morphological operators such as closing and opening and resizing . After cleaning, we use bwlabel() to label the text as we have in the middle frame below. Then we convert to binary to get just the hand written text.

We also use image processing methods, in this case image correlation to find the occurences of a tempalte word, in this case "DESCRIPTION". The images below show the template word and the results of the correlation. The images appear to indicate very roughly the instances of occurence but are not as properly correlated as can be expected.

Evaluation: Since the text is not as clearly isolated and the correlation is not as proper, only 7 out of the possible 10 points is proper.

Acknowledgement: I would like to thank Mr. Cabello for constructive discussions.

Activity 9: Binary Operations

Objectives: To apply image processing techniques to the analysis of binary images and to do area measurement on such images

Tools: Scilab with SIP

Procedure:We start with an image of a sheet of paper with holes randomly punched through, simulating cells in a microscope slide for example.

For computing expediency, cut up the image into nine panels of 256 by 256 pixels each. The images are read in grayscale and are binarized individually using im2bw with their own threshold values. This is done since there are areas of the original image which are darker or lighter than the rest of the image. As such each image needs a different threshold for converted to binary. After conversion, the "salt and pepper" noise on the converted images are removed by morphologically closing and opening the image. We have below the 9 binary images concatenated into a composite image:

Using the bwlabel() function in Scilab, we label each individual hole and blob with a distinct integer. Then we use the find function to search for each of these values. We sum up all the values to find the area of each blob. Below, we have a histogram showing the number of occurences of a range of areas. We see that the most common areas are the small values corresponding to individual holes.

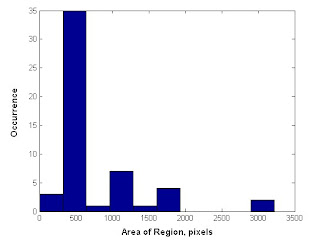
Evaluation: Since the results correlate closely with what is expected, a grade of 10 is proper.

Acknowledgements: I would like to thank Mr. Neil Cabello for his invaluable assistance.

Activity 8: Morphological Operations

Objective: To demonstrate the concepts of image dilation and erosion via a structuring element.

Tools: Scilab with SIP toolbox

Procedure: We use an image set as shown below. The square is 50 by 50 pixels while the hollow square is 60 by 60 and 4 pixels in width. The traingle is 30 by 50 while the circle is 25 pixels in radius. On the other hand, the cross is 8 pixels wide and each arm is 50 pixels long.

ORIGINAL

We use the following structuring elements:

SE1=

1 1 1 1

1 1 1 1

1 1 1 1
DILATION AND EROSION USING SE 1

SE2=

1 1 1 1

1 1 1 1

DILATION AND EROSION USING SE 2

SE3=

1 1

1 1

1 1

1 1

DILATION AND EROSION USING SE 3

SE4=

0 0 1 0 0

0 0 1 0 0

1 1 1 1 1

0 0 1 0 0

0 0 1 0 0

DILATION AND EROSION USING SE 4

We notice distinct changes in the images (which incidentally do not correspond to the predictions made previously). Using a square SE we simply see a transfromation of the structure either as an expansion of the lines in case of dilation and compression with erosion. For the non-symmetric elements( like the 2x4 and 4x2 ones), the expansion or contraction only applies to the elements parallel to the longitudinal axis of the SE. On the other hand, the cross SE yields transformations on both axes as well as the characteristic edge rounding of small SEs.

Acknowledgements: I would like to thank Mr. Cabello and Mr. Panganiban for their assistance.

Evaluation: Since the predictions do not match the result only a grade of 8 is seen as appropriate.

Activity 7:Enhancement in the Frequency Domain

Objectives: To demonstrate the concept of filtering in the frequency domain and how this affect the quality of images.

Tools: Scilab with SIP toolbox

Procedure: We begin by finding the FTs of pairs of apertures such as the ones we have below.

As with the previous activity, the FTs of the various patterns appear as a convolution of the paterns of a single aperture. It is also of note that the Gaussian FT is still a Gaussian but is tranformed in the frequency space. That is, a wider, more spread out Gaussian function has a narrower transform in the FT space.

The next set of examples illustrate the us of filtering in the Fourier space to cancel out certain undesirable components in the images.For example, the image of the moon below has a set of vertical lines which are very pronounced. Also it has some horizontal scan lines which may be an artifact of the mosaic process. In order to remove these, we implement the following steps:

1. Take the FT of the image.

2. Create a mask to remove certain components.

3. Shift (fftshift) the mask so that the lower order componenents are on the outer portions of the image.

4. Multiply the mask and the FT

5. Take the FT of the product. and normalize.

For this image we use a cross shaped filter to cancel out the periodic, cosinusoidal frequencies in the x and y direction. Note that the mask does not cover the DC component as this contains a lot of information about all the points on the object. Hence if it is removed we lose valuable information. The resulting filtered image is shown below the original. Note that the lines have been removed and the image is cleare. However since we inadvertently removed other useful components, the image has less contrast and detail in some parts than the original.

On the other hand, we a decidedly more difficult image with the next one which is a patch from a painting on stretched canvas. The task is to remove the weave pattern to enhance the actual image. For this we work directly with the FT of the image. The bright spots symmetric about either the x or y axis are the frequencies we want to dscard for these indicate periodic, cosinusoidal patterns in image space. Thus we place circular masks at the positions of these points. We see that when such a mask is used to filter the image, we get a weave free image. Also if we now take our mask and use the centers as the locations of bight spots, that is if we invert the mask, then take the FT, we come up with a weave pattern similar to what we removed from the original image.

For the last section, we attempt to enhance the ridges and lines on an image of a fingerprint. From the FT we discern that our region of interest is the band like structure centered about the DC component. We make a mask to leave only this and the DC component. We see that indeed we can recover the medium frequency components and enace the lines while removing most of the high order noise.

Evaluation: Since all the images were adequately enhanced using FT methods, a grade of 10 is applicable.

Acknowledgements: I would like to thank Misters. Garcia, Gubatan, Panganiban and Cabello for their helpful inputs.

Rating: Since all the results tally with what is expected and the images are well filtered, a score of 10 is warranted.

Activity 6: Properties of the 2D Fourier Transform

Objective: To increase familiarity with the various

Tools: Scilab with SIP toolbox.

Procedure:

1. Familiarization of FT of Different 2D Patterns.

Using the same routines as with the previous activity, we take the FTs of the following apertures:
This yields the following FT patterns:

The first two patterns are identical to the ones from the previous activity. The third image is from an annulus and if we compute the far-field diffraction pattern(which is the same as the FT) we see that the result is a difference between two orders of Bessel functions. Hence we see a set of missing orders or fringes. The fourth is essentially the same only now the functions are sinc functions in x and y. The fourth is the double slit pattern at far field. This can be thought of as coherent oscillators interfering with each other. This means that the upper and lower sections cancel each others contribution. This leaves the central strip hence we only see a pattern at the center of the strip. The last image represents two circular apertures, this results in a modulation of the phase from the other hole causing the interfernce fringes that are superposed on the circular diffraction fringes.

2. Anamorphic Property of the Fourier Transform

A. We take a 2-D Sinusoid with frequency f=4:

We then take the FT of this pattern which yields two points in the transform plane. This corresponds to the frequency of the input. We do this for two other frequencies,f=1 and f=15 to get the following images arranged in increasing f:

We see that as the frequency increases, the points move further from the center. This makes sense if we treat the points as the frequncies of the sine waves (which they are). Thus as the frequency is increased the points move away from the center.

Now if we add a constant bias, we essentially add a field with all the possible frequencies present. Hence from Fourier theory, the FT of this is a single point. We see this when we get the mesh() of the biased sine wave. For comparison, we place on the left a mesh plot of the FT of the same wave without a bias:

The spike at the center represents the frequency of the bias or what is known as the zero-order component. Note that this is of a greater intesity than the sine spikes. If in a real image this becomes an issue, it is possible to subtract the constant value from the input image. This would leave the two spikes represnting the sine. The position of the spikes corresponds directly to the frequency hence we can find the spatial frequency of the fringes in areal image. On the other hand, if the bias is not constantand is a low f sine, we can use the FTs and remove the lower frequency component. We can then take the inverse transform to leave us with the filtered sinusoidal wave.

If we rotate the sine waves like the ones below:

We get the following patterns, which are consistent with the previous result:

If we multiply two sines or any function with two frequencies, we get a superposition of the transforms of both. In this case we use a product of two sne functions:

Which has a transform like:

This corresponds with what we expected as we see two sets of spikes which individually look like the pattern for a simple sine function.

For the last part, if wee add this function to the rotated sines above, we get an image which looks like:

Which has a transform like:

All this essentially tells us that the 2D FT obeys the priciple of superposition.

Reference: AP 186 Activity 6 Manual

Evaluation: For the proper results, a grade of 10 is warranted.

Activity 5: Fourier Transform Model of Image Formation

Objective: To introduce the use of the Fourier Transform or FT as the standard model for imaging applications highlighting the varied uses of this method for image processing.

Tools: Scilab with SIP toolbox.

Procedure:The activity is divided into 5 parts each with its own focus.

1. Familiarization with the discrete FFT:
This section focuses on the use of the FFT as the mathematical equivalent of a lens. For this section we use two shapes, a circle and a square as our object and essentially image it with a lens of infinite aperture via the 2-D FFT function:

The corresponding FTs for these are as follows:

These image on the left represents the Airy disk of a point like image and the left image represnts the sinc(x)*sinc(y) function from a square aperture. This is how the patterns will appear on the transform plane on the back focal plane of a lens. Incidentally, these two images represent the far field or Fraunhofer diffraction pattern of the two aperture illuminated by a plane wave. When the FT of these images are taken we get the FT of the FT which are just the original images. On the other hand, if we use as our image a capital letter "A" as we have below:

We get a Fourier transform like the one we have below:
This indicates a center of symmetry even if the original image is only laterally symmetric. We also note that this patten may be thought of as a superposition of many point spread functions interfering with each other thus yielding this complex pattern. If we now take the FT of this image, we get an inverted "A" which can be thought of as the image of the object as seen through a lens system:

2. Convolution-Simulation of an Imaging Device.

The Convolution theorem essentially states that when the transform of two functions are multiplied it is equal to the transform of the product of the original functions. When this is translated into imaging, the image of an object ban be thought of as the convolution of the aperture function and the transfer function of the lens (or any other imaging system). In this case we use the the capital letters "VIP" in white against a blackbackground and a series of circular apertures simulating the aperture stop of the imaging lens. We take the FT of the aperture as imaged by a lens and then multiply it with the aperture which is in the transfrom plane. we then take the FT one more time to simulate another imaging lens.

We use the following apertures with increasing size.

The corresponding imaged convolutions are:

These correspond well to the fact that a larger aperture will produce a clearer image compared to a smaller aperture. At small apertures, the diffraction from the aperture actually limits the resolution of the imaging system.

3. Correlation-Template Matching

The section on correlation utilizes an image with certain text and a template letter. The correlatio is maximum when the section of the image matches completely with the template. This results in a large spot or spread function at the location of the match. In this case, we use the image on the left and then a template for the letter "A." The correlation is displayed on the right of these two:

The bright points indicate the regions of maximum correlation and these correspond clearly with the locations of the letter A in the image on the left.

4. Edge detection using convolution integral

In this last section we use the same concept as template matching to find the edges of an image pattern. This time we use matrices as our teplate instead of imges. Again we use the VIP image and find its edges using the following matrices:

A= -1 -1 -1

2 2 2

-1 -1 -1

B= -1 2 -1

-1 2 -1

-1 2 -1

and

C= -1 -1 -1

-1 8 -1

-1 -1 -1

With the following results:

Reference: AP 186 Activity 5 Manual

Evaluation: For the sheer amount of work expended as well as the proper results a grade of

10 is warranted.

Acknowledgements: I would like to thank the usual people for their assistance.

Activity 4:Enhancement by Histogram Manipulation

Objective: To manipulate images via their corresponding histogram and to enhance images by altering the gray levels as indicated by the histograms.

Tools: Scilab with SIP toolbox.

Procedure: The first order of business is to convert a colored image into grayscale or find a low contrast grayscale image. In this case we use an image of the M17 Nebula taken by the Hubble Space Telescope from the site:

http://www1.cs.columbia.edu/~johnc/ta_page/6998s07/

schedule/proj1/proj1.html

We then take the histogram of this, as in the previous activity, by finding and counting the number of pixels which have a specific grayscale value and plotting these against the actual values. This yields a histogram like this:

We then take another function related to the histogram

called the CDF. This is essentially the cumulative sum

of the histogrm at each grayscale value. This is found simply by using the cumsum() function in Scilab. The CDF of the image above looks like:

In order to enhance the image the idealized CDF for thi

s is a straight, increasing line. Thus after generating such a f

unction, we use projection to replace the grayscale values in the original image with the grayscale values of the y-axis equivalents. This effectively replaces the grayscale values which cause the CDF to deviate from the ideal. The net effect, at least in theory is an increase in the contrast between light and dark regions. However as shown by the new, enhanced image below, the contrast does not change too drastically.

But if we look at the histogram and the CDF of this new image, we see that the new CDF is already ideal:

Additionally, we present other examples of images enhanced using respectively:

Activity 3:Image types and basic image enhancement

Objective: Differentiate image formats and apply basic image processing and conversion.

Tools: Image processing software and Scilab

Procedure: We use several different images:



1. RGBImage of NGC 2392, Eskimo Nebula
Taken from www.hubblesite.org200 x 200 pixels.
72x72 dpi
4kB in RGB

2. GrayscaleImage of M17 Nebula taken by HST

Taken from: http://www1.cs.columbia.edu

/~johnc/ta_page/
6998s07/schedule/proj1/proj1.html
200 x200 pixels
149.987 x149.987 dpi

3. Indexed

Colorized image of the entire sky at

gamma-ray energies

Taken from: http://www.phys.ncku.edu

.tw/~astrolab/mirrors/apod

/ap950623

.html

477x297 pixels

96 x 96 dpi

46.2 kB

Then in order to apply basic image processing techniques, we use a colored image and convert it to binary using a histogram routine to find the appropriate threshold value. Then we use the routine from the previous Activity to find the are of the ROI. Specifically, we use the figure shown below (taken from E. Marolda, The U.S. Navy in the Vietnam War)

This is then converted to binary using the im2bw routine which uses a threshold value to specify the gray level which is converted to either white or black. The following code is used to generate the historgram of the image:

clc
clf

img=imread('C:\Documents and Settings\2005-09860\Desktop\page3_2_en_sub.png');
//imshow(img);
a = 1;

g= [];
p= [];
for j = 1:256
[x, y] = find(img== j);
g(a) = j;
p(a) = length(x);
a = a + 1;
end
subplot(211)
//p=p/max(max(p));

plot(g,p)

-----------------------------------------------------------------------------------------------------
After conversion, the area of the image is taken using the routine in the previous activity. The routine indicates that this image has an are of 84500.5 units. Compared to the previous images processed, this appears to be a fairly accurate result.

Evaluation:For the effort expended and the acceptable result I can rate this as a 10.

Acknowledgements:I would like to thank Mr. Gubatan for insights on the histogram process as well as the usual folks for their assistance.

References: AP 186 Activity 3 Manual

Activity 2:Area estimation for images with defined edges

Objective: Use image processing software and Green's Theorem to compute the area of a regular polygon and compare this with the analytically computed area.

Tools: Scilab specifically the Image Processing Toolbox, MS Paint

Procedure: We use four different regular shapes drawn in black and white using MS paint.

These have areas of 10285, 6545, 5676 and 42121 square units respectively. Using the "follow" command in Scilab, we can get the x and y coordinates of the contour forming the border of the black and white regions. This creates two arrays of numbers called X and Y.

We then use a "for" loop to substitute these values of X and Y into the equation:where x and y are the coordinate arrays and the index i is the length of the array. This code is implemeted as follows:
______________________________________________________________
clc
clf

fig=imread('C:\Documents and Settings\2005-09860\Desktop\circ.bmp');
fig=im2bw(fig,0.5);
imshow(fig);

[x,y]=follow(fig);

i=length(x);
a=[];

for j=1:i-1
a(j)=x(j)*(y(j+1))-y(j)*x(j+1);
end

Area=sum(a)/2

______________________________________________________________

This code outputs a number which corresponds to the are of the polygon.

Results:

The following results were obtained using the shapes above:


These results correspond closely with the computed values. With the exception of the triangle, the deviations were all below 5% which indicates consistency. The triangle area may have a larger difference due to the manner in which a diagonal line is drawn in MSPaint. The line is drawn as a series of steps instead of a straight line.

Acknowledgements: I would like to thank the usual people for their help.

Refernces: AP 186 Activity 2 Manual.

Rating: For this Activity, the acceptable correlation of the results with the actual values allow for a rating of 10.

Activity 1: Digital Sacnning

Objective: Use ratio and proportion to find the numerical values of a hand-drawn (or machine printed) plot.

Tools: MS Paint, Spreadsheet, image processing software

Description of procedure: We start with an scanned image of an old plot from some journal.

Figure 1. Original image of the plot.

We then take a fixed interval in an axis of the plot (which corresponds to a physical value) and note the number of pixels comprising this interval in the image. This give us a ratio of the physical quantity per pixel. For example, if the plot shows 100 units in the x axis and consists of 200 pixels in the image, we get a ratio of:


100 units/ 200 pixel= 0.5 units per pixel

We do this for both a and y axes. We then take the coordinates of the points in the plot and copy these into a spreadsheet. Using the ratios we derived earlier, we can then get the values corresponding to the physical quantities for both x and y axes. When these are plotted and the graph axes are adjusted to reflect the scale on the image, we get a plot that should correspond to the original drawing as we see below.

Figure 2. Overlay of origial plot and the plotted points from spreadsheet.

Comments: The results correspond well to the curve on the image. Note that the plotted points are represented as squares on the plot above. The main difficulty encountered is the scaling and the correlation of the axes which turns out to be a bit trickier than anticipated.

Source: Wood and Petrie, "Nitrogen metabolism of plants," Annals of Botany, Vol 2. 1938.

Acknowledgements: I would like to thank Doctors Soriano and Perez for their instruction. Also I would like to thank Misters Cabello, Dilla, Garcia, Gubatan and Villoan for their invaluable assistance.

Evaluation: For this activity I give mysely a grade of ten (10) for my output is quite acceptable and that the procedure for this exercise was thoroughly understood.

Additional Image: Trendline from spreadsheet showing logarithmic fit (compare with original scanned line)

First Post

Read the tiltle.