Activity 17: Photometric Stereo

Objectives: To reconstruct a three dimensional image using a set of 2-D images with different illumination positions.

Tools: Scilab with SIP.

Procedure: We start with four images of a spherical calibration target illuminated by a point source at these locations:

S1 = (0.085832, 0.17365, 0.98106)

S2 = (0.085832, -0.17365, 0.98106)

S3 = (0.17365, 0, 0.98481)

S4 = (0.16318, -0.34202, 0.92542)

The positions vary by very small increments and hence the images do not appear to be any different to the eye. We find the surface normal vector to the points on the surface using the equation:

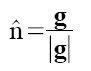
Where g is given by:

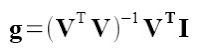
With V taken from the images. The slope with respect to z of each point in both x and y is given by:

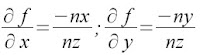
The function f is fiven by the sum of the integrals of the partials in x and y. Numerically we use the cumulative sum fucntion to find these integrals and the resulting funtion is plotted in 3-D. The result is somehting like the plot below:

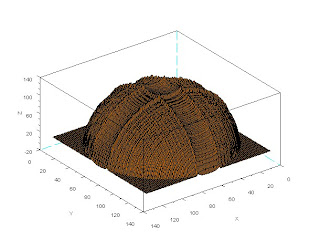
As we can see, the plot is hemispherical which is the result expected. It is of interest to examine the effect of varying the illumination shift on the accuracy of the reconstruction. It is also of note that this approach is from the stanpoint of intensity. That is, the changes in the illumination allow for the measurement of slope and shape. Another approach may involve the phase of the illuminating light which has been shown to yield better results in terms of reconstruction ability.

Evaluation: For the proper reconstruction of the shape, a grade of 10 is appropriate.

Acknowledgements: The assistance of Neil Cabello and Earl Panganiban is greatly appreciated.